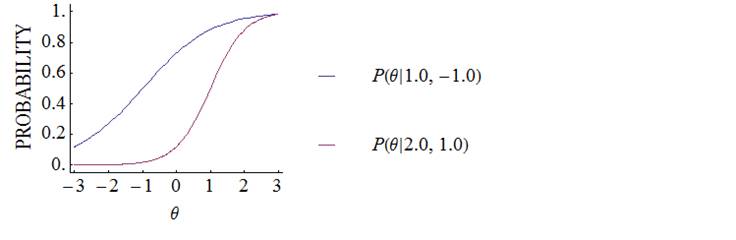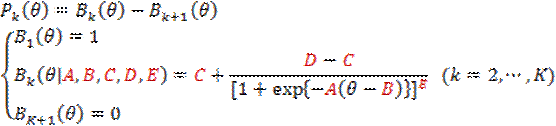Item Response Theory
Data Format	Model Type
	2-Parameter Model	3-Parameter Model	4-Parameter Model	5-Parameter Model
Dichotomous
Nominal-Polytomous
Ordered Polytomous
Continuous
Dichotomous Model
Dichotomous IRT models are used for binary true/false data.
2-Parameter Logistic Model The 2-parameter logistic (2PL) model is a dichotomous IRT model in which the shape of the item response function (IRF) is represented by two parameters: slope (A) and location (B). The probability that an examinee with ability θ correctly answers an item is expressed as The IRF increases/decreases monotonically when A is positive/negative and becomes steeper as A becomes larger. In addition, the larger the B, the more positively the IRF is located.
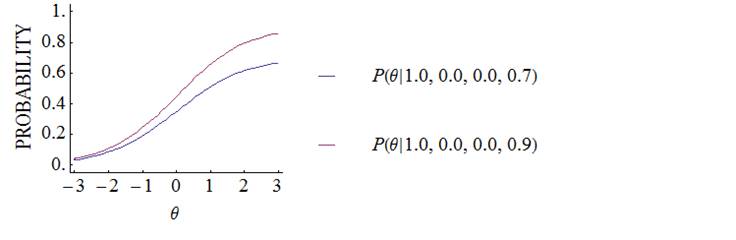
3-Parameter Logistic Model The 3-parameter logistic (3PL) model is a dichotomous IRT model in which a lower asymptote parameter (C) is added to the 2PL model. The lower limit of the IRF becomes larger as C becomes larger.
4-Parameter Logistic Model The 4-parameter logistic (4PL) model is a dichotomous IRT model in which an upper asymptote parameter (D) is added to the 3PL model. The upper limit of the IRF becomes larger as D becomes larger.
5-Parameter Logistic Model The 5-parameter logistic (5PL) model is a dichotomous model in which an asymmetry parameter (E) is added to the 4PL model. Although, the IRF is point symmetrical with respect to point (B, P(B)) when E is 1.0, it becomes negatively skewed as E approaches zero and positively skewed as E increases from 1.0.
Bock’s Nominal Model
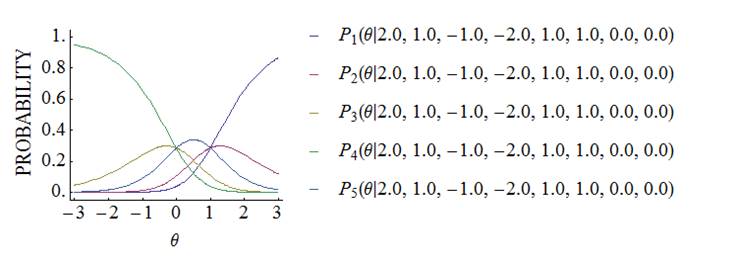
Bock’s nominal IRT model can be used to simultaneously examine a correct choice and incorrect choices. When the number of categories is K, the item category response function (ICRF) of the nominal model is expressed as Although it is difficult to practically interpret the parameter values, the ICRF with the largest A is most positively located. In addition, the parameter estimates become more stable if categories with a small number of selections are integrated into one category. Bock, R. D. (1972) Estimating item parameters and latent ability when responses are scored in two or more nominal categories. Psychometrika, 37, 29-51.
Samejima’s Graded Model
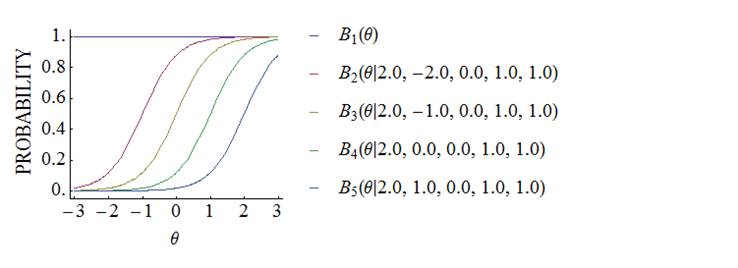
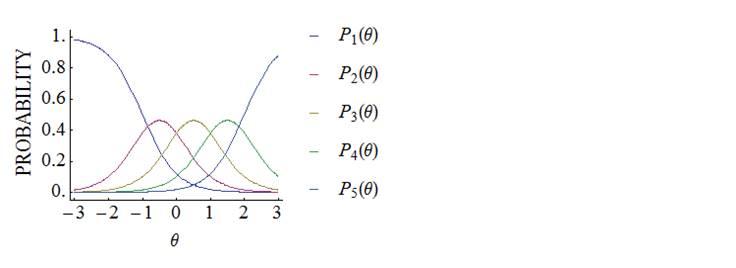
Samejima’s graded IRT model can be used to analyze psychological rating scale (Likert scale) data. When the number of categories is K, the ICRF of the graded model is given by The Bk(θ) is called the boundary category response function (BCRF); it represents the probability of selecting category k or higher. The ICRF can be selected from the 2- to 5-parameter logistic models. Samejima, F. (1969) Estimation of latent ability using a response pattern of graded scores. Psychometrika Monograph, No.17.
Analysis Setting
Estimation Model l The default model is the dichotomous model. l Specify the “dichotomous model” when analyzing binary true/false data. l Specify “Bock’s nominal model” when analyzing correct and incorrect choices. l For the nominal model, the categories with a small number of selections should be merged into one category. l Specify “Samejima’s graded model” when analyzing psychological rating scale (Likert scale) data.
Model Parameters l The default setting for the dichotomous model is the 3-parameter model. l Only the 2-parameter model can be specified for the Bock’s nominal model. l The default setting for Samejima’s graded model is the 3-parameter model.
Equating (Parameter Fixing Sheet) l Equating is executed using the concurrent calibration (CC) method. l The CC method is used to estimate the parameters of only the equated items (the parameters of the remaining items are fixed).
Output Options
Fit Indices l Fit indices for the complete test and each item are output. l Output indices ・Chi-square (df, p-value) ・NFI (normed fit index; Bentler & Bonnet, 1980) : [0, 1] the larger, the better ・RFI (relative fit index; Bollen, 1986) : [0, 1] the larger, the better ・IFI (incremental fit index; Bollen, 1989) : [0, 1] the larger, the better ・TLI (Tucker-Lewis index; Bollen, 1989) : [0, 1] the larger, the better ・CFI (comparative fit index; Bentler, 1990) : [0, 1] the larger, the better ・RMSEA (root mean square error of approximation; Browne & Cudeck, 1993) : [0, ∞] the smaller, the better l Information criteria are relative indices to compare two or more model candidates. The smaller the value, the more efficient the fit of the model to the data. ・AIC (Akaike information criterion; Akaike, 1987) ・CAIC (consistent AIC; Bozdogan, 1987) ・BIC (Bayesian information criterion; Schwarz, 1978)
IRF Graphs l The IRF and item information function for each item are graphed. l The ICRF for each item is also graphed when the nominal model is specified. l The ICRF and BCRF for each item are also graphed when the graded model is specified. l The test response function and test information function are graphed.
Sorting by Correct Response Rate l In worksheet “Items”, the output items are sorted in descending order of correct response rate. l In worksheet “Items”, the output items are sorted in descending order of mean value when the graded model is specified.
Go to Main Page